2. Ecological theory¶
2.1. Levels of ecology¶
Ecology covers a vast range of topics and can be viewed on multiple levels. One level is that of the individual organism—a single bacterium, an individual wolf pup. This includes individual behavior and physiology, with behavior as part of ecology. Population ecology covers groups of organisms of the same species—a bison herd or a grove of maples. Community ecology looks at how different populations interact, and the communities examined can be quite large. Above this level is ecosystem ecology, which examines how different communities interact with their environments. Finally, there is global ecology—ecology of the planetary ecosystem.
Level |
Description |
|---|---|
Individual ecology |
Single organisms, behavior, and physiology |
Population ecology |
Groups of organisms from a single species |
Community ecology |
Populations of interacting species |
Ecosystem ecology |
Multiple communities and the environment |
Global ecology |
The planet as a biosphere |
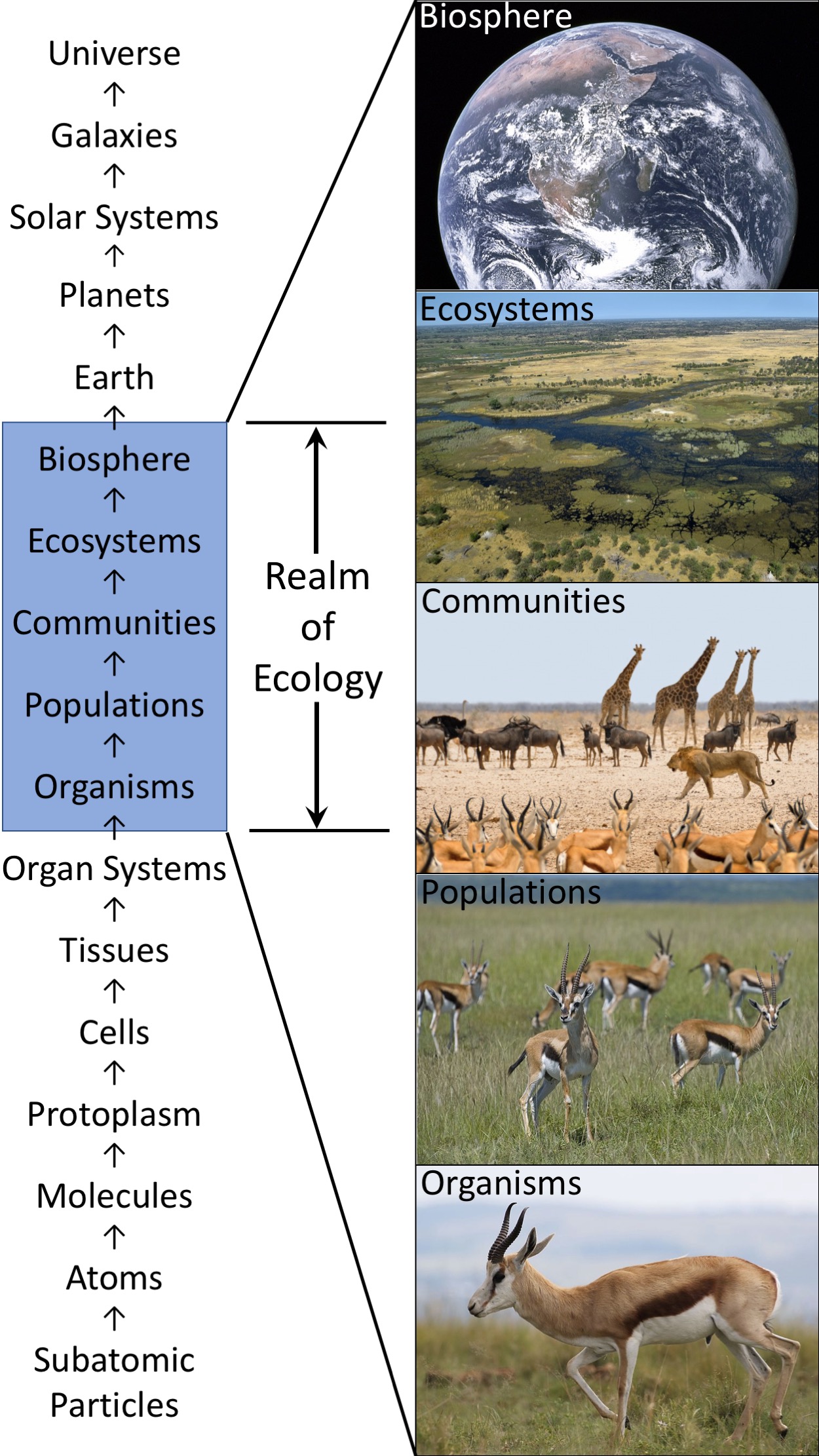
Fig. 2.1 Levels of complexity Levels of complexity by Multiple authors see Quantitative Ecology for licensing ¶
2.2. Role of theory¶
From its early days, ecology has been in part a theoretical–mathematical science, and it is now also a computational science. Mathematical theory arises where systems are relatively simple. In our modern era, computation can address somewhat more complex systems, though creating computations on complex systems that satisfy the basic tenets of science is still problematic. For very complex systems, narrative is all we have available.
Examine the levels in Fig. 2.1 to think about where theory applies. Subatomic particles and atoms are the realm of quantum mechanics, one of the most sublime and successful theories. Theory applies nicely to the hydrogen atom, a two-particle object. And while it applies to larger atoms, the raw mathematics becomes too complex as the number of particles grows, so computation comes into play. At higher levels like the molecular one, theory is harder to apply. Organic chemistry, for example, is not a strongly mathematical science, and at the level of protoplasm and cells there is no comprehensive mathematical theory or computational equivalent. This level is far too complex – with minuscule molecular machines running along tubules and carrying mitochondria on their backs at high speed relative to their size, it is more complex than any industrial factory. At the level of tissues and organs systems, we have only narratives to guide our understanding.
What happens, then, at the level of organisms, at the entry to ecology? Individual organisms are exceedingly complex. There is no complete mathematical theory for the internal operation of individual organisms. But externally, organisms behave as a unit and populations become simpler than individuals – glossing over heartbeat, neuron firing rates, white blood cell replication, and so on, with all their enormous complexity. Details disappear. Populations can be described with basic mathematics. Communities are more complex, but are still within the reach of mathematics and, particularly, within the reach of computation. And ecosystems are complex, but with some unifying properties.
The whole earth thus begins to be simpler, and at the level of planets and solar systems, things once again become nicely mathematical. This is the level where, with Newton, modern science was born. In part, this emerging simplicity is because levels of detail again merge together. At the level of planetary orbits, it does not matter that dinosaurs once dominated the planet or that Mozart ever wrote any concertos.
At larger scales still, solar systems are completely describable with computers, although the mathematics becomes difficult, and as we move out into galaxies and the entire universe the descriptions become difficult again.
Changing scales thus involves the successive movement in and out of simplicity. Where is the complexity in the universe greatest? It turns out to be at about one meter. In other words, at our scale. A great spike in complexity appears just where we and other forms of life arose.
That is no accident. A philosophical idea called the weak anthropic principle suggests that any part of the universe that can sit around and contemplate itself and the larger universe must itself be complex. We are constrained to live at a scale of great complexity, or not to exist at all. That is worth some reflection.
But we try to find simplicity among this complexity, to let us feel we understand, and to let us predict what can happen.
2.3. What is a model?¶
Science strives for simplicity, and models are part of the process. What is a model? It is just a simplified view of something more complex.
The word “model” is used here essentially as it’s used in everyday English. For example, in ordinary English, “modeling clay” can be used to make simplified miniatures of three-dimensional images of animals, automobiles, buildings, or even full-scale three-dimensional images of objects like the human heart.
A “model airplane” can be rendered to show at a glance the physical appearance of a large aircraft, and can even be constructed to fly so as to test aerodynamics under proper rescaling. A “model organism” is a simpler organism that may respond to medical tests or treatments in ways similar to those of a more complex organism.
Even the fashion model on the runway meets this definition of a simplified view of something more complex. The infinite complexity of the human spirit is not relevant on the runway; all that is relevant in this context is the person as a realistic way to display fashions.
This book focuses on computational and mathematical models of ecological systems. What is left out of these models is as important as what is put in. Simplification is key.
If you have a complex natural system you don’t understand, and you construct a computer model incorporating everything you can about that natural system, you now have two systems you don’t understand.
—after Chris Payola, UMN
A designer knows he has achieved perfection not when there is nothing left to add, but when there is nothing left to take away.
—Antoine de Saint-Exupery
Two different simplifications of time are commonly used in ecological models:
Discrete time: Events happen at periodic time steps, as if time is non-existent in between.
Continuous time: Events happen smoothly and at all times.
In addition, there are two different classes of models:
Macroscale: Individual organisms are not tracked, but are measured in aggregate and represented by composite variables such as \(N\).
Microscale: Individual organisms are tracked separately. These are also known as agent-based or individual-based models.
Macroscale models can be handled either by computers or mathematics, but microscale models are usually restricted to computers. Keep in mind that all four categories are only approximations of reality.
Later in this book we will also explore mechanistic versus phenomenological models.
2.4. Present state¶
As a surprising side note, the standard models commonly taught in ecology courses are not complete, and a main purpose of this book is to help make them more so. One aspect of theory related to simple species, for instance – called orthologistic population growth – is rarely even studied, much less taught, yet is essential for understanding rapidly growing populations, including human populations in millennia past. For two-species interactions, another theory concerning mutualisms and a related kind of population growth is highly under-developed, and the theory of three-species interactions is even less complete.

Fig. 2.2 The eternal mystery of the universe is its comprehensibility – Albert Einstain Einstein by Lucien Chavan (Public Domain) ¶
